Beginning with the May 1993 issue I did a three-part column discussing my method of predicting the performance of prospective electric models. I received quite a bit of mail from readers about my theories and formulas. Just about everyone who wrote either applied my formulas to their models or shared their own flight prediction systems, and I'd like to pass some of their ideas along to you.

     Let's review my method of determining flight performance. First, figure the wing loading in ounces per square foot. Next, compute the power-to-weight ratio by dividing the input power (watts in, figured by multiplying the battery voltage by the current draw) by the ready-to-fly weight (ounces). Finally, find the Aircraft Performance Ratio (APR) by dividing the power-to-weight ratio by the wing loading. The APR will indicate the model's expected flight performance according to the ranges listed below:

     Using these parameters to evaluate performance has worked well for me, but fellow Model Builder columnist Francis Reynolds wrote with some suggestions on how to make these indicators even better. He notes that characterizing an aircraft's performance based on wing loading leads to inconsistencies among models of different sizes.
     As an example, the flight characteristics of an 05-size J-3 Cub with a wing loading of 25 ounces per square foot are much different than a larger 40-size Cub with the same wing loading. As another example, the large Telemaster is a nice and slow trainer aircraft even though its wing loading can be between 20 and 40 ounces per square foot. A wing loading this high on a small plane would make it impossible to use as a trainer. Clearly, there is a difference in flying characteristics between small planes and large planes with identical wing loadings; there should be a way to compensate for this disparity.
     Ted Off, in an article in RCM around 1987, explains what happens to an aircraft when its size is changed relative to scale speed, wing loading and engine size. Although his theoretical discussion does not go far enough, his next analytical step is that wing loading should be measured by a cubic term, not a squared term as in square feet of wing area.
     Francis took the next step in a series of columns in Model Builder describing the Wing Cube Loading (WCL) parameter. It is found by dividing the traditional wing loading (ounces per square foot) by the square root of the wing area (square feet).

IMPORTANT NOTE: December 2021 - The formula in the preceding paragraph is NOT the same formula as in the Francis Reynolds article.

Reynold's formula: wing cube loading (WCL)= weight in ounces (oz.) divided by (/) wing area in feet raised (^) to the 1.5 power

Jaffe's formula from above: Wing Cube Loading (WCL) = wing loading in ounces per square foot (oz./sq.ft.) divided by (/) the square root of the wing area (sq.ft.) raised (^) to the 0.5 (Raising to the 0.5 is another way to calculate the square root of a number and yields the same result as using the square root key on a calculator.)

Example for the full size Cub Example below:

Typical Wing Loading: weight in ounces (oz.) divided by (/) wing area in square feet (sq.ft.) - 17,600 oz. / 178 sq.ft. = 98.876404 oz./sq.ft.

Reynolds: 17,600 oz. / 178 sq.ft.^1.5 = 17,600 / 2374.8162 = 7.4110999

Jaffe: 98.876404 oz./sq.ft. / 178 sq.ft. ^ 0.5 = 98.876404 / 13.341664 = 7.4110999

Keep in mind that either formula yields the same result!

     Francis claims that every J-3 Cub from a very small model to a full-size one will have about the same wing cube loading. Let's test him!
     A full-size Cub has a wing area of 178 square feet and a typical flying weight of 1,100 pounds (17,600 ounces), therefore, the wing loading figures at 98.876 ounces per square foot; dividing this by the square root of the wing area (13.34) equals 7.41 ounces per cubic foot.

IMPORTANT NOTE: February 2018 - There should be no units attached to the Wing Cube Loading (WCL) value. See my Personal Comment, added in February 2018, to Francis Reynolds article. It is easy to locate my comment as it is also in a blue font. As you continue reading this article, ignore any reference to ounces per cubic foot.

     My ElectriCub model weighs 50 ounces and the wing area is 429 square inches. Plugging everything into the equation gives a WCL of 9.72 ounces per cubic foot. The Goldberg Anniversary Edition Cub (gas power) has a wing area of 744 squares and a ready-to-fly weight of 120 ounces; its wing cube loading is 10.2 ounces per cubic foot.
     Although it may appear that the WCL parameters diverge between different size aircraft, let's tabulate the WCL alongside the traditional wing loading:

     The difference in WCL numbers is insignificant compared to the difference in wing loading numbers, particularly between the two models and the full-size plane. As you can see, Francis has normalized the size difference between planes of the same type.
     Next, using his aeronautical background and his experience, Francis categorizes planes according to their wing cube loading:

Type of Aircraft Wing Cube Loading
Gliders 4
Trainers 6
Sport Aerobatic 9
Pattern 11
Racers 12
Scale 10-15
Full-Scale 15-20

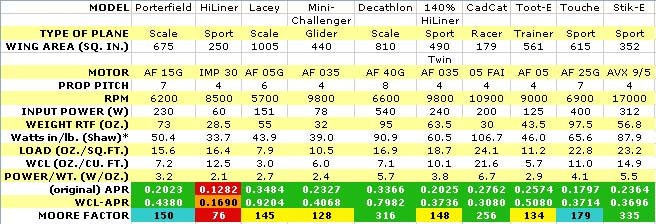
     Computing the WCL parameters for various models as shown in Figure 1, I have to agree with Francis in his analysis of wing cube loading because each plane's type and its WCL category are consistent.

WCL-APR Performance
Less than 0.150 No-Go
0.150-0.170 Marginal
0.170-0.200 Fair
0.200-0.300 Good
Greater than 0.300 Excellent

     I like the WCL parameter; using the WCL and the WCL-APR parameters for my electric aircraft analysis is more accurate than the regular wing loading parameter because it does what Francis says it's supposed to, normalize the size variations of aircraft.

     Rod Moore of Canoga Park, California and I have carried on a lively debate about this subject since my last set of articles. His aircraft performance number uses a different set of parameters that I want to share with you.
     To compute Rod's performance factor, first compute the input power-to-weight ratio (in watts per pound) and then multiply it by the ratio of estimated flight speed and estimated stall speed. The estimated flight speed in miles per hour is found by multiplying the prop pitch times the prop speed and dividing by 1,000. The estimated stall speed in miles per hour is found by taking the square root of the wing loading and multiplying by 3.7. Rod categorizes his performance factor numbers like this:

     Figure 1 lists Rod's performance factor for each of the planes, as you can see, it's right on the money. This is another electric aircraft performance factor that works very well in judging flight performance.

     Renowned electric flight master Keith Shaw has his own method of evaluating aircraft performance; it was published in the July 1987 issue of Model Builder. It is more of a design tool, since it's used in the early stage of designing and analyzing an electric model. It's too long to fully restate here, but if you want the full details, look up the issue or send me an SASE and I'll send you a copy.

Summarizing, here's how he does it:
     Using Keith's guidelines, choose a suitable wing loading appropriate for the design and size of the model you want to build. With this wing loading value, compute the finished weight by multiplying wing loading by the wing area. Also using Keith's guidelines, compute the power required to fly the plane, then the static current drain and the battery cell count. Next, decide if you should gear the motor or stick to direct drive. Now you can estimate the proper flying speed and stall speed and the correct propeller diameter and pitch. Finally, after subtracting the weight of the motor, batteries and radio from the estimated ready-to-fly weight, ask yourself if you can build the model for that amount of weight.

     Now that we have three methods from which to choose, let's take a look at the similarities and differences between them. With Rod's and Keith's methods you need to know the rpm and the prop pitch for the kind of motor you want to use. This isn't so hard to do, particularly if you've been reading the electric columns for a few months. Not a month goes by that there isn't some motor and prop speed data. I've compiled a list of motor and propeller data I've saved over the years it's yours for an SASE. Of course, if you really don't have any idea about the speed and power of your motor, you can always test the system on your workbench.
     Rod's predictor is different than my new predictor (using the WCL-APR parameter) in a couple of ways. His uses weight to the11/2 power whereas mine is weight squared, making mine more sensitive to changes in weight. Increasing the weight will make my predictor less favorable than his. Also, Rod's predictor uses the square root of wing area; mine uses area to the three-halves power (A3/2) changing the wing area will reflect more in my predictor than his. Therefore, my predictor is more sensitive to changes in weight and wing area. For the most part this is all right, but in some cases my method fails because of its sensitivity.
     Rod's method and my method take the known and estimated parameters from a given plane (wing area, finished weight, motor power, etc.) and compute a performance indicator. Keith's method turns the whole analysis around and first asks what kind of performance you want from your plane, then determines what the parameters should be the wing loading, how much it should weigh, how many cells to use and what size prop to swing. Obviously each method has proven its worth, since all of us have used them to accurately predict aircraft performance.